1 集成学习
科学研究中,有种方法叫做组合,甚是强大,小硕们毕业基本靠它了。将别人的方法一起组合起来然后搞成一个集成的算法,集百家之长,效果一般不会差。其实也不能怪小硕们,大牛们也有这么做的,只是大牛们做的比较漂亮。
在PAC学习框架下(Probably Approximately Correct), Kearns和Valiant指出,若存在一个多项式级的学习算法来识别一组概念,并且识别正确率很高,那么这组概念是强可学习的;而如果学习算法识别一组概念的正确率仅比随机猜测略好,那么这组概念是弱可学习的。Schapire证明了弱学习算法与强学习算法的等价性问题,这样在学习概念时,只要找到一个比随机猜测略好的弱学习算法,就可以将其提升为强学习算法,而不必直接去找通常情况下很难获得的强学习算法。这为集成学习提供了理论支持。
在众多单模型中(与集成模型相对应),决策树这种算法有着很多良好的特性,比如说训练时间复杂度较低,预测的过程比较快速,模型可解释强等。但是同时,单决策树又有一些不好的地方,比如说容易over-fitting,虽然有一些方法,如剪枝可以减少这种情况,但是还是不够的。
集成学习还是有很多方法的,在这里只介绍两种普遍做法:bagging集成和boosting集成。bagging集成,例如随机森林,对样本随机抽样建立很多树,每棵树之间没有关联,这些树组成森林,构成随机森林模型。boosting集成后一个模型是对前一个模型产生误差的矫正。gradient boost更具体,是指每个新模型的引入是为了减少上个模型的残差(residual),而为了消除残差,我们可以在残差减少的梯度(Gradient)方向上建立一个新的模型。如果基础模型是决策树,那么这样的模型就被称为Gradient Boost Decision Tree(GBDT)
2 XGBoost
GBDT可以看做是个框架,最早的一种实现方法由Friedman 在论文GREEDY FUNCTION APPROXIMATION: A GRADIENT BOOSTING MACHINE 。xgboost(eXtreme Gradient Boosting)是最近提出的一个新的GBDT实现,由陈天奇提出,在Kaggle、KDD Cup等数据挖掘比赛中大方异彩,成为冠军队伍的标配,另外很多大公司,如腾讯、阿里、美团已在公司里面部署。XGBoost有如下优点:
- 显示的把树模型复杂度作为正则项加到优化目标中。
- 公式推导中用到了二阶导数,用了二阶泰勒展开。
- 实现了分裂点寻找近似算法。
- 利用了特征的稀疏性。
- 数据事先排序并且以block形式存储,有利于并行计算。
- 基于分布式通信框架rabit,可以运行在MPI和yarn上。
- 实现做了面向体系结构的优化,针对cache和内存做了性能优化。
3 监督学习要素
XGBoost应用于监督学习问题,使用训练数据(有很多特征)$x_i$来预测目标$y_i$。 监督学习的三要素:模型、参数和目标函数
3.1 模型
模型指给定输入$x_i$如何去预测输出$y_i$。我们比较常见的模型如线性模型(包括线性回归和logistic regression)采用了线性叠加的方式进行预测$\hat{y}_i=\sum_j w_j x_{ij}$. 其实这里的预测$y$可以有不同的解释,比如我们可以用它来作为回归目标的输出,或者进行sigmoid 变换得到概率,或者作为排序的指标等。而一个线性模型根据$y$的解释不同(以及设计对应的目标函数)用到回归,分类或排序等场景。
3.2 参数
参数指我们需要学习的东西,在线性模型中,参数指我们的线性系数$w$。
3.3 目标函数
模型和参数本身指定了给定输入我们如何做预测,但是没有告诉我们如何去寻找一个比较好的参数,这个时候就需要目标函数登场了。一般的目标函数包含下面两项:

其中$L$为训练损失函数,$\Sigma$是正则项,惩罚模型复杂度。 常见的损失函数,对于回归问题,有损失函数L为最小平方误差: $L(y, \hat{y}) = (y - \hat{y})^2$,对于二分类,损失函数L为logit loss $L(y, \hat{y})=-log\,\sigma(y, \hat{y})$ 为什么加入正则项?因为模型是在训练集上训练,但是实际应用时时另一份数据集,一般为测试集。那么模型在训练集上表现优异,不代表在测试集上会好。越是在训练集上模型越是复杂,则模型过拟合会比较严重。
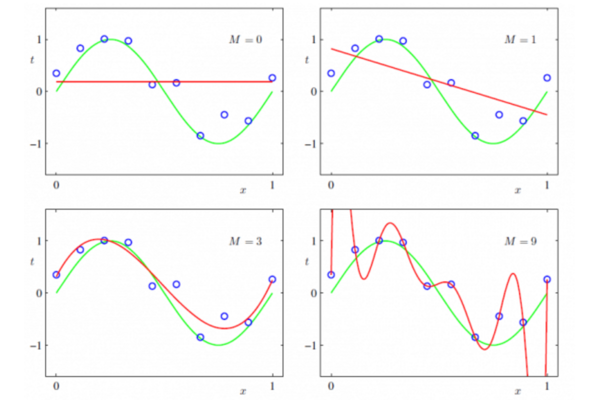
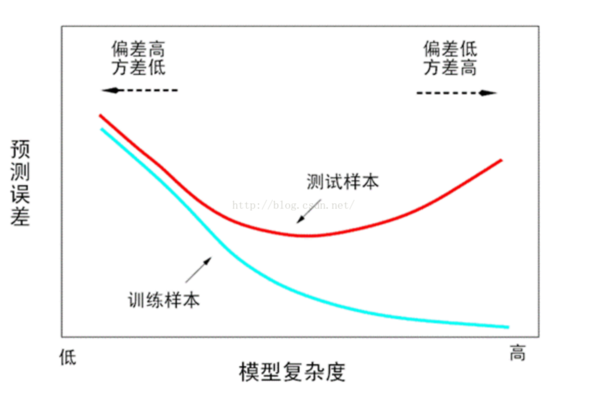
奥卡姆剃刀原则:在所有可能选择的模型中,能够很好解释已知数据,并且十分简单的模型才是最好的模型。总而言之,加入正则项是为了提高模型的泛化能力,既在未知数据集上同样表现良好。 常见的正则化项有L1正则和L2正则。L1正则项是参数向量的L1范数,L2正则项是参数向量的L2范数
4 Boosted Tree
4.1 基学习器CART
Boosted tree 最基本的组成部分叫做回归树(regression tree),也叫做CART。
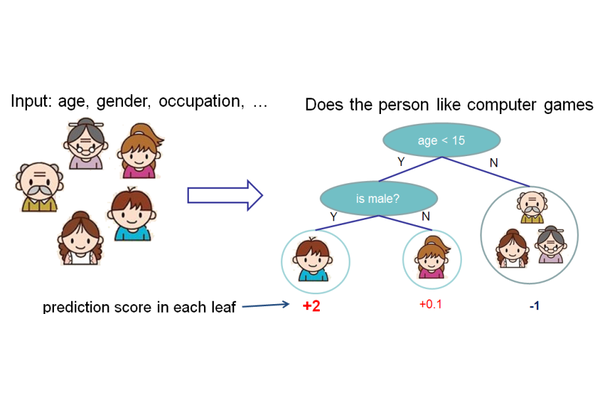
上面就是一个CART的例子。CART会把输入根据输入的属性分配到各个叶子节点,而每个叶子节点上面都会对应一个实数分数,你可以把叶子的分数理解为有多可能这个人喜欢电脑游戏。
CART树模型的参数是什么?树的参数一般为树的结构、树的叶子节点、叶子节点的值等
4.2 Tree Ensemble
一个CART往往过于简单无法有效地预测,因此一个更加强力的模型叫做tree ensemble。
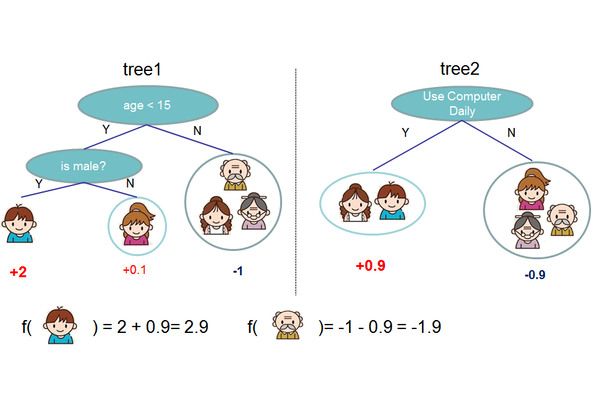
在上面的例子中,我们用两棵树来进行预测。我们对于每个样本的预测结果就是每棵树预测分数的和。 Tree ensemble一般写法为:
\[\begin{equation} \hat{y_i}=\sum_{k=1}^K f_k(x_i), f_k \in \mathcal{F} \end{equation}\]其中$K$为树的棵树,每个$f$是一个在函数空间$\mathcal{F}$里面的函数,$\mathcal{F}$对应了所有CART树的集合。在XGBoost里面的目标函数也由两部分构成:损失函数+正则项,既:
\[\begin{equation} Obj(\Theta)=\sum_i^n l(y_i,\hat y_i) +\sum_{k=1}^K\Omega(f_k) \end{equation}\]其中$n$为样本数目.
4.3 模型学习
目标函数的第一部分是训练误差,也就是大家相对比较熟悉的如平方误差, logistic loss等。而第二部分是每棵树的复杂度的和(这部分在下面介绍)。现在我们的参数可以认为是在一个函数空间里面,我们不能采用传统的如SGD之类的算法来学习我们的模型,因此我们会采用一种叫做additive training的方式。每一次保留原来的模型不变,加入一个新的函数$f$到我们的模型中。
\[\begin{equation} \begin{split}\hat{y}_i^{(0)} &= 0\\ \hat{y}_i^{(1)} &= f_1(x_i) = \hat{y}_i^{(0)} + f_1(x_i)\\ \hat{y}_i^{(2)} &= f_1(x_i) + f_2(x_i)= \hat{y}_i^{(1)} + f_2(x_i)\\ \hat{y}_i^{(t)} &= \sum_{k=1}^t f_k(x_i)= \hat{y}_i^{(t-1)} + f_t(x_i) \end{split} \end{equation}\]$\hat{y}_i^{(t)}$为第$t$轮的模型预测,$\hat{y}_i^{(t-1)}$保留前面$t-1$轮的模型预测,$f_t(x_i)$新加入的函数
现在还剩下一个问题,我们如何选择每一轮加入什么$f$呢?答案是非常直接的,选取一个$f$来使得我们的目标函数尽量最大地降低。
\[\begin{equation} \begin{split}\text{obj}^{(t)} &= \sum_{i=1}^n l(y_i, \hat{y}_i^{(t)}) + \Omega(f_t) \\ &= \sum_{i=1}^n l(y_i, \hat{y}_i^{(t-1)} + f_t(x_i)) + \Omega(f_t) + constant \end{split} \end{equation}\]如果$L$为平方误差的情形下,目前函数可以写成
\[\begin{equation} \begin{split}\text{obj}^{(t)} &= \sum_{i=1}^n (y_i - (\hat{y}_i^{(t-1)} + f_t(x_i)))^2 + \sum_{i=1}^t\Omega(f_i) \\ &= \sum_{i=1}^n [2(\hat{y}_i^{(t-1)} - y_i)f_t(x_i) + f_t(x_i)^2] + \Omega(f_t) + constant \end{split} \end{equation}\]更加一般的,对于不是平方误差的情况,我们会采用如下的泰勒展开近似来定义一个近似的目标函数,方便我们进行这一步的计算。

当我们把常数项移除之后,我们会发现如下一个比较统一的目标函数。这一个目标函数有一个非常明显的特点,它只依赖于每个数据点的在误差函数上的一阶导数和二阶导数. 误差函数为
\[\begin{equation} \sum_{i=1}^n [g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i)] + \Omega(f_t) \end{equation}\]一阶导数、二阶导数为
\[\begin{equation} \begin{split}g_i &= \partial_{\hat{y}_i^{(t-1)}} \; l(y_i, \hat{y}_i^{(t-1)})\\ h_i &= \partial_{\hat{y}_i^{(t-1)}}^2 \; l(y_i, \hat{y}_i^{(t-1)}) \end{split} \end{equation}\]4.4 模型复杂度
先将$f$的定义做一下细化,把树拆分成结构部分$q$和叶子权重部分$w$。结构函数$q$把输入映射到叶子的索引号上面去,而$w$给定了每个索引号对应的叶子分数是什么。
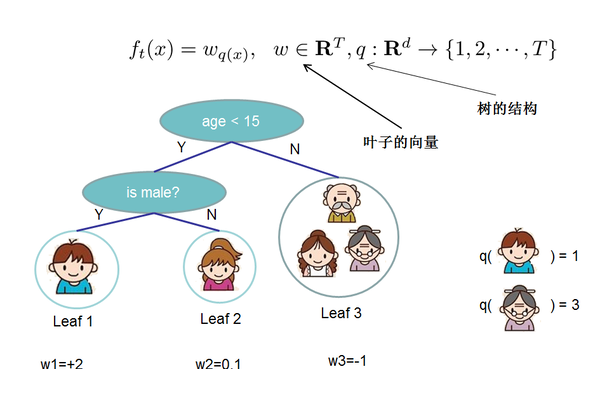
给定了如上定义之后,树的复杂度为:
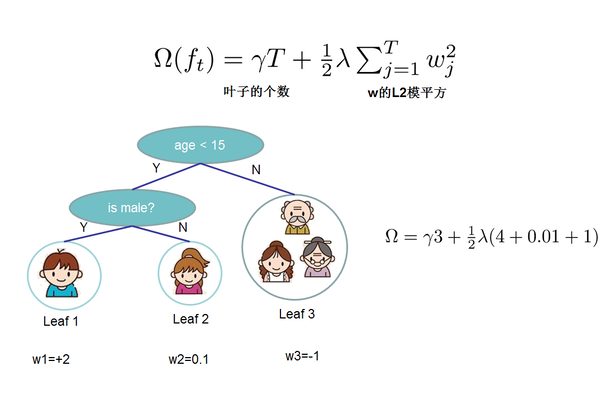
这个复杂度包含了一棵树里面节点的个数,以及每个树叶子节点上面输出分数的$L2$模平方。当然这不是唯一的一种定义方式,只是这种方式简单并且有效。
树的结构
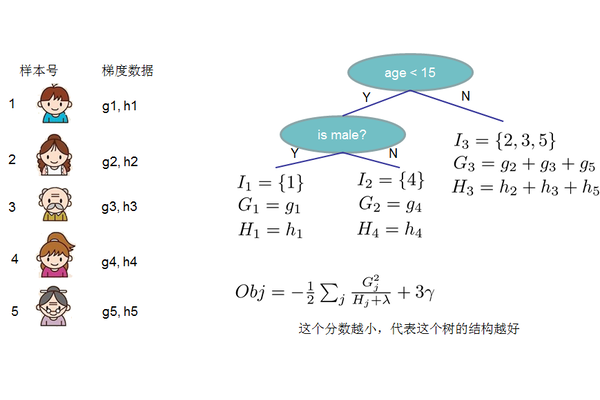
根据$q$和$w$的定义,目标函数可以改写成,其中$I$被定义为每个叶子上面样本集合$I_j = {i|q(x_i) = j} $
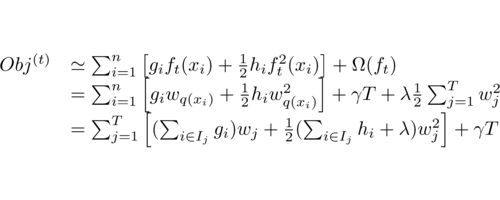
定义$G_j = \sum_{i \in I_j} g_i \quad H_j = \sum_{i \in I_j} h_i$,那么这个目标函数可以进一步改写成如下的形式
\[\begin{equation} \begin{split} Obj^{(t)} &= \sum_{j=1}^T [( \sum_{i \in I_j} g_i)w_j+\frac 1 2(\sum_{i \in I_j} h_i + \lambda)w_j^2] + \gamma T \\ &= \sum_{j=1}^T [G_j w_j + \frac 1 2 (H_j + \lambda) w_j^2] + \gamma T \\ \end{split} \end{equation}\]假设我们已经知道树的结构$q$,我们可以通过这个目标函数来求解出最好的$w$,以及最好的$w$对应的目标函数最大的增益。上面的式子其实是关于$w$的一个一维二次函数的最小值的问题 ,求解既得到
\[\begin{equation} \begin{split} w_j^* &= - \frac {G_j} {H_j + \lambda} \\ Obj &= - \frac 1 2 \sum_{j=1}^T \frac {G_j^2} {H_j + \lambda} + \gamma T \end{split} \end{equation}\]Obj表示在某个确定的树结构下的结构分数(structure score),这个分数可以被看做是类似gini、information gain(一般决策树评分函数)一样更加一般的对于树结构进行打分的函数。
4.5 学习树结构
4.5.1 Exact Greedy Algorithm
直观的方法是枚举所有的树结构,并根据上面数structure score来打分,找出最优的那棵树加入模型中,再不断重复。但暴力枚举根本不可行,所以类似于一般决策树的构建,XGBoost也是采用贪心算法,每一次尝试去对已有的叶子加入一个分割。对于一个具体的分割方案,增益计算如下:
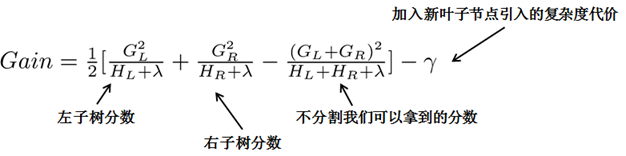
对于每次树的扩展,需要枚举所有可能的分割方案,如何高效地枚举所有的分割呢?假设要枚举所有 $x< a$这样的条件,对于某个特定的分割$a$,要计算$a$左边和右边的导数和。
对于所有的$a$,首先根据需要划分的那列特征值排序,然后从左到右的扫描就可以枚举出所有分割的梯度和$G_L$和$G_R$,再用上面的公式计算每个分割方案的分数就可以了。

上面是针对一个特征,如果有m个特征,需要对所有参数都采取一样的操作,然后找到最好的那个特征所对应的划分。

上图是论文中原图,我理解input d(feature dimension)应该为m
4.5.2 Approximate Algorithm
如果是分布式计算,则需要更好的方法。XGBoost还提出了分布式情况下的分割算法:
分布式近似建树将在下面一篇博文中详细描述。
4.5.3 Sparsity-aware Split Finding
实际的项目中的数据一般会存在缺失数据,因此在寻找最佳分割点时需要考虑如何处理缺失的特征,作者在论文中提出下面的算法

对于特征k,在寻找split point时只对特征值为non-missing的样本上对应的特征值进行遍历,不过统计量$G$和$H$则是全部数据上的统计量。在遍历non-missing的样本$I_k$时会进行两次。按照特征值升序排列遍历时实际是将missing value划分到右叶子节点,降序遍历则是划分到左叶子节点。最后选择score最大的split point以及对应的方向作为缺失值的default directions.
参考资料
- http://www.kdd.org/kdd2016/papers/files/rfp0697-chenAemb.pdf
- http://www.52cs.org/?p=429
- http://xgboost.readthedocs.io/en/latest/model.html
- https://homes.cs.washington.edu/~tqchen/pdf/BoostedTree.pdf
- http://gaolei786.github.io/statistics/prml1.html 过拟合
- http://dataunion.org/9512.html
- http://www.cnblogs.com/leftnoteasy/archive/2011/03/07/random-forest-and-gbdt.html
- https://statweb.stanford.edu/~jhf/ftp/trebst.pdf
