1. 近似分割算法
XGBoost解读(1)–原理中介绍了XGBoost使用exact greedy算法来寻找分割点建树,但是当数据量非常大难以被全部加载进内存时或者分布式环境下时,exact greedy算法将不再合适。因此作者提出近似算法来寻找分割点。近似算法的大致流程见下面的算法。

对于某个特征$k$,算法首先根据特征分布的分位数找到切割点的候选集合\(S_k = \{s_{k1}, s_{k2}, ... ,s_{kl} \}\);然后将特征$k$的值根据集合$S_k$划分到桶(bucket)中,接着对每个桶内的样本统计值$G$、$H$进行累加统计,最后在这些累计的统计量上寻找最佳分裂点。从算法伪代码可以看出近似算法的核心是如何根据分位数采样得到分割点的候选集合$S$. 本文接下来的内容也是围绕这个进行阐述。
2. Quantile
2.1 $\phi$-quantile
Quantile就是ranking。如果有N个元素,那么$\phi$-quantile就是指rank在$\lfloor \phi \times N \rfloor$的元素。例如$S=[11, 21, 24, 61, 81, 39, 89, 56, 12, 51]$,首先排序为$[11, 12, 21, 24, 39, 51, 56, 61, 81, 89]$,则0.1-quantile=11, 0.5-quantile=39. 上面的是exact quantile寻找方法,如果数据集非常大,难以排序,则需要引入$\epsilon$-approximate $\phi$-quantiles
2.2 $\epsilon$-approximate $\phi$-quantiles
也就是$\phi$-quantile是在区间$[ \lfloor (\phi - \epsilon) \times N \rfloor, \lfloor (\phi + \epsilon) \times N \rfloor]$。还是上面的例子,领$\epsilon=0.1$,则有0.2-quantile={11, 12, 21}
3. Weighted Datasets
回到XGBoost的建树过程,在建立第$i$棵树的时候已经知道数据集在前面$i-1$棵树的误差,因此采样的时候是需要考虑误差,对于误差大的特征值采样粒度要加大,误差小的特征值采样粒度可以减小,也就是说采样的样本是需要权重的。
重新审视目标函数
\[\begin{equation} \sum_{i=1}^n [g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i)] + \Omega(f_t) \end{equation}\]通过配方可以得到
\[\begin{equation} \sum_{1}^n \left[ \frac {1}{2} h_i \left( f_t(x_i) - (-g_i/h_i)\right)^2 \right] + \Omega (f_t) + constant \end{equation}\]因此可以将该目标还是看作是关于标签为${-{g_i}/{h_i}}$和权重为$h_i$的平方误差形式。
论文中$\frac{g_i}{h_i}$前面没有负号,可是通过推导我认为这种形式才是对的。当然这边的符号不影响论文中其他表达的正确性
3.1 二阶导数h为权重的解释
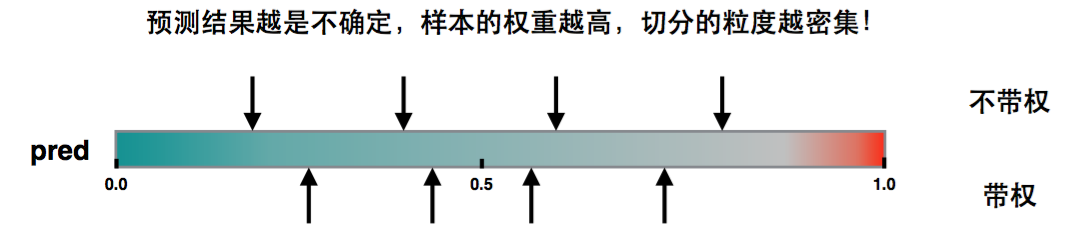
如果损失函数是Square loss,即$Loss(y, \widehat y) = (y - \widehat y)^2$,则$h=2$,那么实际上是不带权。 如果损失函数是Log loss,则$h=pred* (1 - pred)$. 这是个开口朝下的一元二次函数,所以最大值在0.5。当pred在0.5附近,这个值是非常不稳定的,很容易误判,h作为权重则因此变大,那么直方图划分,这部分就会被切分的更细
3.2 问题转换
记
\[\begin{equation} D_k = \{(x_{1k}, h_1), (x_{2k}, h_2), \cdots (x_{nk}, h_n)\} \end{equation}\]表示 每个训练样本的第$k$维特征值和对应二阶导数。接下来定义排序函数为$r_k(\cdot):R \rightarrow[0, +\infty)$
\[\begin{equation} r_k (z) = \frac {1} {\sum\limits_{\left( {x,h} \right) \in {D_k}} h } \sum\limits_{\left( {x,h} \right) \in {D_k},x < z} h \end{equation}\]函数表示特征的值小于$z$的样本分布占比,其中二阶导数$h$可以视为权重,后面论述。在这个排序函数下,我们找到一组点\(\{ s_{k1}, s_{k2}, ... ,s_{kl} \}\) ,满足:
\[\begin{equation} | r_k (s_{k,j}) - r_k (s_{k, j+1}) | < \varepsilon \end{equation}\]其中,\({s_{k1}} = \mathop {\min }\limits_i {x_{ik}},{s_{kl}} = \mathop {\max }\limits_i {x_{ik}}\)。$\varepsilon$为采样率,直观上理解,我们最后会得到$1/\varepsilon$个分界点。
对于每个样本都有相同权重的问题,有quantile sketch算法解决该问题,作者提出Weighted Quantile Sketch算法解决这种weighted datasets的情况。具体算法描述和推理在论文的补充材料。
4. Weighted Quantile Sketch
4.1 Formalization
给定一个multi-set \(D = \{ (x_1, w_1), (x_2, w_2), \cdots (x_n, w_n)\}\), \(w_i\in [0, +\infty], x_i \in \mathcal{X}\). 如果数据集D是根据$\mathcal{X}$上的升序进行排列,作者定义了两个rank function
\[\begin{equation} \begin{split} r_{D}^{-} = \sum_{(x, w)\in D, x<y} w \\ r_{D}^{+} = \sum_{(x, w)\in D, x\leq y} w \end{split} \end{equation}\]注意到$D$是个multi-set,因此会有一些数据具有相同的$x$和$w$,作者还定义了weight function
\[\begin{equation} \begin{split} w_{D}(y) = r_{D}^{+}(y) - r_{D}^{-}(y) = \sum_{(x,w)\in D, x=y}w \end{split} \end{equation}\]样本集合D上的全部权重定义为\(w(D) = \sum_{(x, w)\in D} w\)
4.2 Quantile Summary of Weighted Data
根据上面定义的概念和符号引出Quantile Summary of Weighted Data的定义 数据集$D$上的quantile summary被定义为\(Q(D) = (S, \tilde{r}_{D}^{+}, \tilde{r}_{D}^{-}, \tilde{w}_{D})\), 其中集合\(S=\{ x_1,x_2,..., x_k\}\)从D中选出($x_i\in {x|(x_w)\in D}$). S中的元素需要满足下面的性质:
- \(x_i < x_{i+1}\) 对所有的$i$成立。并且$x_1$和$x_k$分别是$D$中的最小和最大点:
- 函数\(\tilde{r}_{D}^{+}, \tilde{r}_{D}^{-}, \tilde{w}_{D}\) 是定义在集合$S$上的函数,并且满足
4.3 $\varepsilon$-Approximate Qunatile Summary
给定的quantile summary \(Q(D)=(S, \tilde{r}_{D}^{+}, \tilde{r}_{D}^{-}, \tilde{w}_{D})\), $Q(D)$被称为$\varepsilon$-Approximate Qunatile summay,当且仅当 \(\tilde{r}_{D}^{+}(y)-\tilde{r}_{D}^{-}(y)-\tilde{w}_{D}(y) \leq \varepsilon w(S)\) 对于任意一个$y\in X$成立. 意思也就是说我们对\(r_{y}^{+}\)、\(r_{y}^{-}\)的估计的最大error至多为\(\varepsilon w(D)\).
4.4 构建$\varepsilon$-Approximate Qunatile Summary
4.4.1 初始化
在小规模数据集\(D = \{ (x_1, w_1), (x_2, w_2), \cdots (x_n, w_n)\}\) 上构建初始的quantile summary \(Q(D) = (S, \tilde{r}_{D}^{+}, \tilde{r}_{D}^{-}, \tilde{w}_{D})\),集合$S$满足:\(S=\{x|(x,w)\in D\}\). \(\tilde{r}_{D}^{+}, \tilde{r}_{D}^{-}, \tilde{w}_{D}\)被定义为
\[\begin{equation} \tilde{r}_{D}^{-}(x) = r_{D}^{-}(x) \\ \tilde{r}_{D}^{+}(x) = r_{D}^{+}(x) \\ \tilde{w}_{D}(x) = w_{D}(x) \end{equation}\]可以看出,初始的$Q(D)$是0-approximate summary.
4.4.2 Merge Operation
\(Q(D_1)=(S_1, \tilde{r}_{D_1}^{+}, \tilde{r}_{D_1}^{-}, \tilde{w}_{D_{1}})\)和\(Q(D_2)=(S_1, \tilde{r}_{D_2}^{+}, \tilde{r}_{D_2}^{-}, \tilde{w}_{D_{2}})\)分别定义在数据集$D1$和$D2$上,令\(D=\{D_1\cup D_2\}\),那么merged summary \(Q(D)=(S, \tilde{r}_{D}^{+}, \tilde{r}_{D}^{-}, \tilde{w}_D)\)被定义为:
\[\begin{equation} \begin{split} S=\{(x_1, x_2, ..., x_k)\}, \quad x_i\in S_1 \quad or \quad s_i \in S_2 \\ \tilde{r}_{D}^{-}(x_i) = \tilde{r}_{D_1}^{-}(x_i) + \tilde{r}_{D_2}^{-}(x_i) \\ \tilde{r}_{D}^{+}(x_i) = \tilde{r}_{D_1}^{+}(x_i) + \tilde{r}_{D_2}^{+}(x_i) \\ \tilde{w}_{D}(x_i) = \tilde{w}_{D_1}(x_i) + \tilde{w}_{D_2}(x_i) \end{split} \end{equation}\]4.4.3 Prune Operation
给定\(Q(D)=(S, \tilde{r}_{D}^{+}, \tilde{r}_{D}^{-}, \tilde{w}_{D})\) (其中\(S=\{x_1, x_2, ..., x_k\}\))和memory budget $b$,prune operation构建一个新的summary, \(\acute{Q}(D)=(\acute{S}, \tilde{r}_{D}^{+}, \tilde{r}_{D}^{-}, \tilde{w}_{D})\). \(\acute{D}\)中的\(\tilde{r}_{D}^{+}, \tilde{r}_{D}^{-}, \tilde{w}_{D}\)定义与原先的summary $Q$一致,只是定义域从$S$变为\(\acute{S}\), \(\acute{S}=\{\acute{x_1}, \acute{x_2}, ..., \acute{x_{b+1}}\}\), $\acute{x_i}$的选择按照下面的操作获取:
\[\begin{equation} \acute{x_i}=g(Q, \frac{i-1}{b} w(D)) \end{equation}\]$g(Q, d)$是query function,对于给定的quantile summary $Q$和rank $d$, $g(Q, d)$返回一个元素$x$,$x$的rank最接近$d$,具体定义为

参考资料
- http://www.kdd.org/kdd2016/papers/files/rfp0697-chenAemb.pdf
- http://homes.cs.washington.edu/~tqchen/pdf/xgboost-supp.pdf
- http://datascience.stackexchange.com/questions/10997/need-help-understanding-xgboosts-approximate-split-points-proposal